article
Few-shot learning: How to build AI that is “Curiously” fast at learning new concepts
We are innovating machine-learning models that only need a handful of examples to learn a new concept in dialogues
May 26, 2022 • 11 minutes
Imagine this task: Given a sentence requesting a seat purchase, we want to identify, say, the seat number — a machine-learning task more generally known as Named Entity Recognition (NER). Here is an example input sentence:
- “I want to purchase seat 13A.”
The answer is readily obvious to our smart human brains: “13A”. But what if I asked you to explain how to arrive at such a decision to a robot?
- Would the explanation be to choose any number followed by a letter? Then what about “13A” in a sentence like “I live at 7 Cool St. Apt. 13A”?
- Would it be to choose any alphanumeric word following the word seat? Then what about, “I want to purchase seat number 13A”?
We could continue grinding down this path, but it is already clear that exhaustively specifying rules for how to identify the seat number is not going to work. Somehow, we just know that “13A” is the seat number, even if we cannot put this knowledge into words.
Enter, Deep Neural Networks
Deep Neural Networks (DNNs) — inspired by how the human brain works — are among the most flexible methods for picking up complex patterns in data. Coming back to the above example, we can simply show a DNN many sentences in which the seat number is identified, and the DNN will discover what patterns in a sentence would correspond to a seat number. In other words, it will learn all different combinations of words that could precede and/or follow a word to make that word become a seat number. The training of a DNN to do NER is more involved than that, but this abstraction is solid enough for our discussion here. See this post for how the actual training is carried out.
This unparalleled power to learn patterns, combined with the ongoing revolution in the availability of data and computational power, has placed DNNs at the heart of almost all applications in the broader intelligence domain. From computer vision (like detecting objects in images), to answering questions in natural language, to discovering new medicine, and more. However, there is a caveat to DNNs’ power. If DNNs can pick up on any pattern, what prevents them from picking up on the wrong patterns? The answer is the amount of training data.
The key word in our previous discussion of training a DNN to identify the seat number was many. The DNN needs to see many sentences in order for us to have some guarantees that it will not pick up spurious patterns.
For example, imagine we show the DNN only the following two sentences with their annotated seat numbers in bolded font:
- “I want to purchase seat 13A.”
- “Can I change my seat 7K on flight number 29C?”
The DNN will successfully avoid the spurious pattern that “any number followed by a letter is a seat number” due to the presence of 29C as not a seat number. However, it will learn another spurious pattern that “any alphanumeric word following the word seat is a seat number.” Consequently, it will fail on these sentences:
- “I want to purchase seat number 13A.”
- “Can I upgrade my seat on my NYC to Boston trip? 29C is my flight number and 13A is my seat.”
There are many spurious patterns to avoid, and that is why DNNs need to be trained on many data points. Exactly how many? That is still an open question, and is the central subject of the research on generalization bounds [Neyshabur et al. 2017, Valle-Perez & Louis 2020], but we will leave that discussion for another post. For now, we want to ask a perhaps more interesting and critical question: Should we abandon DNNs altogether if we don’t have enough data for a task? Or can we still make use of their pattern recognition power? Fortunately, the latter is true (with a grain of salt), and in the remainder of this post we will discuss how.
Understanding few-shot learning with a swiss roll
To better understand the problem of training DNNs with only a few annotated samples, commonly known as “few-shot learning,” let us consider a toy problem. In this problem, our goal is to learn to distinguish blue circles from red crosses. Here is the all-knowing oracle description of the underlying data distribution:
The data is sampled from a swiss roll in the 2D cartesian plane, as shown in Figure 1 (left). So each data point is a tuple of (x, y) coordinates. Considering the center as the origin, any point that happens before the length of 5 on the swiss roll is defined to be a blue circle (highlighted in blue), and any point after the length 5 is defined to be a red cross (highlighted in red).
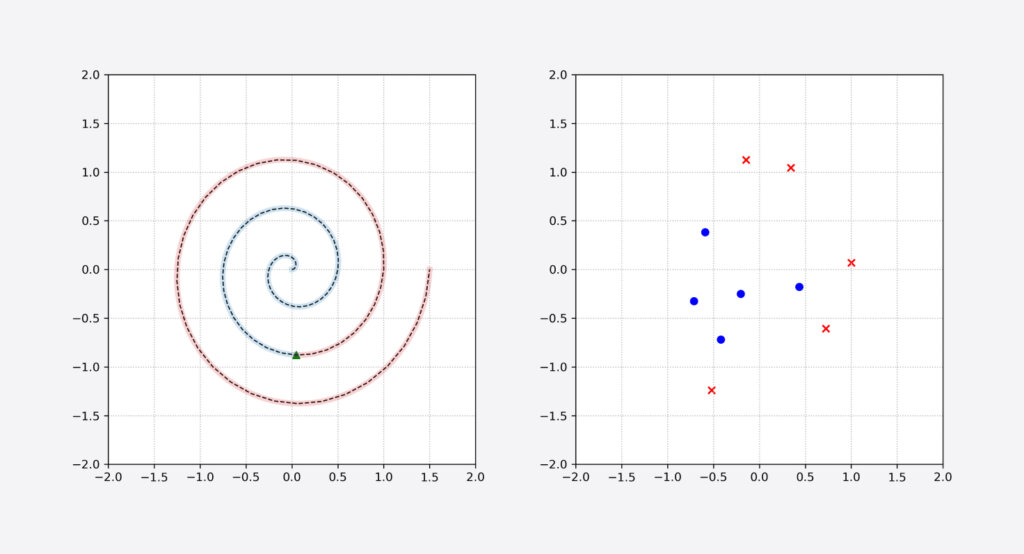
However, we as ordinary humans, do not know what the oracle knows, and just have access to 10 random observations from this distribution. (Think of this as collecting 10 annotations in the NER task, and circles and crosses as being a seat number or not.) Hence, we have a few-shot learning problem.
We observe, by chance, 5 blue circles and 5 red crosses as shown in Figure 1 (right). Our task is a simple two-class classification: We want to learn to distinguish circles from crosses in general, given only the 10 annotated samples we have observed so far. In other words, we want to separate the blue and red highlights in Figure 1 on the left, given only the training samples shown in Figure 1 on the right.
More formally, we represent each data point with a variable z, and its label with a variable c. We want to learn the probability of being a blue circle given any input data point (think of this as the probability of a particular location on a particular sentence being the seat number), that is, p(c|z).
To that end, we use a DNN to model p(c|z), a differentiable function that receives a data point z as input and produces a categorical distribution over labels c. Then we optimize the parameters of this DNN to maximize the likelihood of our observations — log likelihood in practice to speed up the optimization. Figure 2 shows what the DNN would learn (light blue shade shows the region where the DNN classifies inputs as blue circles, i.e. p(c=circle|z) > p(c=cross|z)).
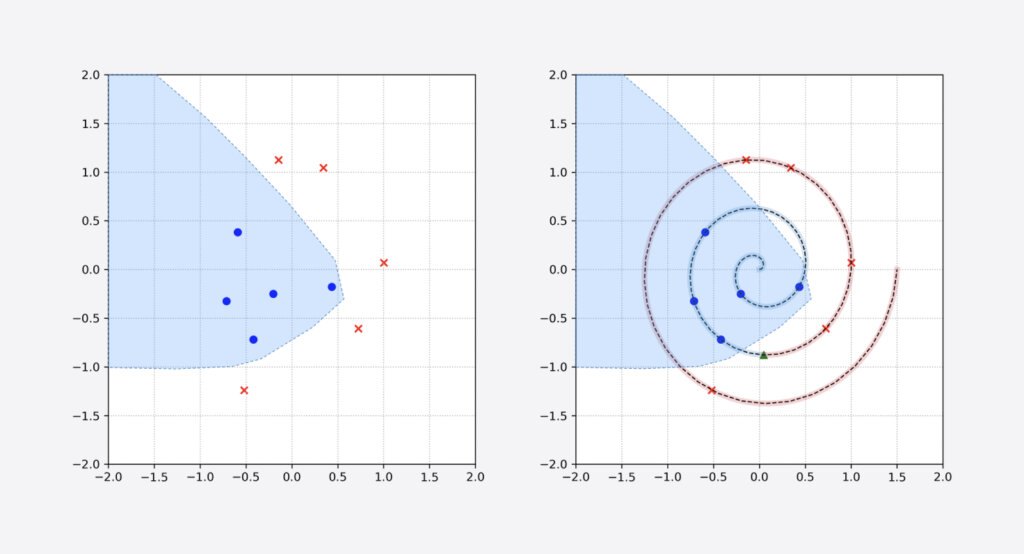
Comparing the true swiss roll distribution with the DNN prediction in Figure 2, it is readily evident that the DNN will make many mistakes. In other words, the model has picked up a spurious pattern for distinguishing blue dots and red crosses. So what can we do about this?
There are two broad ideas for how to improve the few-shot learning challenge and help the DNN learn a better estimate of p(c|z). First, we need to “tell” the DNN that the data is coming from a swiss roll (representation learning). Second, we need to construct new data points through applying specific variations to the existing data points, variations that we know will not change a circle data point to a cross data point or vice versa (data augmentation).
Using representation learning to simplify the task
In the broad sense, representation learning is the idea to use cheaply available, possibly unannotated data (black dots in Figure 3 left) to figure out the best representation for the data. In our toy problem, this means learning that the data is coming from a swiss roll, and that we can therefore represent our data points by the distance from origin on this particular swiss roll.
The details of how to actually learn the best representation from unlabeled samples is subject to active research, but suffice it to say that it is possible to learn such representations. In our toy example, that amounts to converting any data point from a tuple of the form (x, y) to a scalar d showing the distance to origin on the swiss roll (the length of the roll up to that data point). This new representation will simplify the machine-learning task for the DNN as it now has to only figure out the location of the boundary on the swiss roll. This allows the DNN to learn the prediction shown in Figure 3 (right).
Note that even though this new DNN is still imperfect (see how it has over-estimated the boundary between classes in Figure 3), it is performing much better than the previous DNN in Figure 2, even though both are trained on the same number of annotated samples.
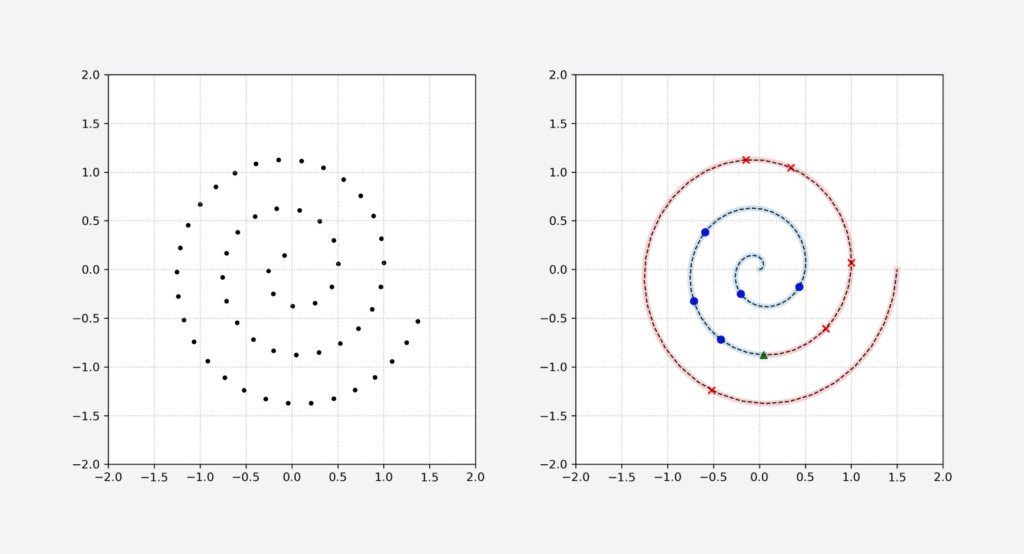
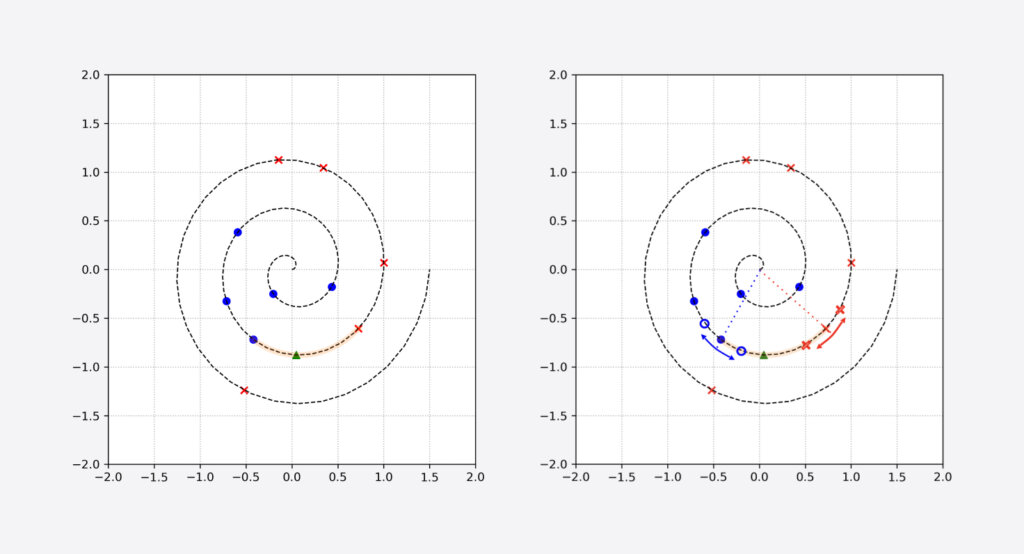
Representation learning can only bring us so far. Looking at Figure 3 (right), we see that the DNN will still make a significant number of mistakes due to the fact that it does not have enough training data to pinpoint the exact location of the boundary between the two classes of circles and crosses. As far as the DNN knows, the boundary can be anywhere in the region of confusion highlighted in yellow in Figure 4 (left). This is where data augmentation comes into play.
Expanding the training data with data augmentation
In data augmentation, the idea is to use our heuristic expert knowledge about the behavior of data to construct additional labeled samples. In our toy problem, let’s say we somehow know that if we slightly move a data point along the arc of a circle centered at origin and radius equal to the distance of the data point to the origin, the class of the data point won’t change. Applying this rule to all existing data points in a training set means we can create many new data points, and shrink down the region of confusion.
An example of applying such a transformation to two points near the region of confusion to construct new data points is shown in Figure 4 (right). These new training data points, along with the first approach of representation learning, enable the DNN to learn a much sharper boundary.
Back to reality
The two ideas discussed above are widely used in real-world applications to tackle few-shot learning problems.
On the representation learning front, the state-of-the-art in the natural language domains are transformer-based models such as BERT [Devlin et al. 2018] and its lighter variants [Lan et al. 2019, Choromanski et al. 2020] that are trained on unannotated sentences to predict randomly masked words or the masked next sentence. As by-products, they learn a good representation of the underlying language structure. This is analogous to learning that the data is coming from a swiss roll, and the distances on this swiss roll are much more “meaningful” for distinguishing different concepts.
On the data augmentation front, it is an open question how to meaningfully augment natural language in different tasks [Feng et al. 2021]. Some popular heuristics include concatenating sentences, translating to another language and translating back, or using word and phrase synonyms.
At LivePerson, we are actively developing new representation learning and data augmentation methods specialized for improving few-shot learning models on dialogue data. Our latest efforts focus on combining representation learning and data augmentations for dialogues into a single iterative method that uses data augmentation to learn better representations and, in turn, uses these representations to discover new symmetries of the data distribution to exploit for further augmentations. This will allow us to cut down on our data sample and annotation requirements for training DNNs, which allows rapid development of models for recognizing new emerging intents in dialogues, identifying scarce entities, and beyond — toward building AI that would not need any more training examples than a human would to recognize a new concept.

